BQ #6: Unit U

1. What is a continuity? What is a discontinuity?

A continuous function is a function is predictable, has no discontinuities (breaks, jumps, or holes), and it can be drawn without lifting you pencil. That just means that the function will go wherever you expect it to and its graph is a smooth line with every value of x having a value. In addition, if the function is continuous, then the intended height of the graph (limit) will equal the the actual height of the graph (value).

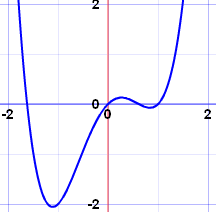(http://www.mathsisfun.com/calculus/continuity.html)

A discontinuity would therefore be where the function is not continuous, where all the breaks, jumps, or holes are. That would make the limit of the graph not equal to the value of the function. There are two families of discontinuities: removable and non-removable. The only removable discontinuity is point discontinuity, which we have previously known as a hole. The three non-removable discontinuities are jump discontinuity, oscillating behavior, and infinite discontinuity. They are grouped as non-removable discontinuities because it is only at those 3 discontinuities that the limit DOES NOT EXIST (DNE). The limit still exists at a hole because the function still intended to go to that point, but it actually didn't. The limit doesn't exist at a jump discontinuity because the left and right limits do not match and for infinite discontinuity, there exists a vertical asymptote which results in unbounded behavior.

 

     Not Continuous             Not Continuous           Not Continuous
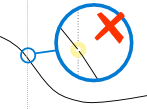
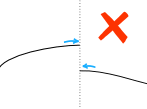
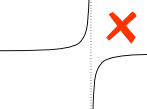
             (Hole)                           (Jump)             (Infinite/Vertical Asymptote/Unbounded Behavior)

Oscillating behavior is just when the graph gets all "wiggly". The graph doesn't have a limit because it doesn't approach any single value.

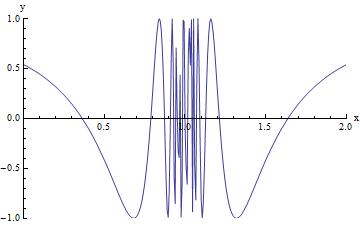(http://www.cwladis.com/math301/indeterminateforms.php)

2. What is a limit? When does a limit exist? When does a limit does not exist? What is the difference between a limit and a value?

A limit is the intended height of the function.A limit only exists when the left and right side limits match each other (or when they meet). That is why a limit still exist at a point discontinuity; the left and and right hand limits are the same number because that is where both sides intended to go. A limit doesn't exist at the 3 non-removable discontinuities because either their left and right limits don't match, of unbounded behavior, or of oscillating behavior.A limit, as stated before, is the intended height of a graph, while the value is the actual height the graph reaches.

(Limit DNE b/c left and right limits don't match)                       (Limit DNE b/c unbounded behavior)

(http://www.cwladis.com/math301/indeterminateforms.php)

                                                      (Limit DNE b/c oscillating behavior)

3. How do we evaluate limits numerically, graphically, and algebraically?

One way to evaluate limits is numerically, meaning using a table. We simply put the number that x is approaching in the middle of the table, add and subtract 0.1 from that number for the two outermost values, and slowly work our way towards that number. Then, we can just use a calculator to figure out the f(x) values on the graph at those x-values. The middle f(x) value should be blank because unknown, but if we compare the the values approaching the number from the left and right, we see that the values are approaching a certain number, which will be where the limit is. Depending on the function though, the limit might or might not be reached.

To evaluate limits graphically, we simply use...a graph. We could use a graphing calculator or if we are given the graph, we can use our left and right hands to see if the right and left hand side meets. With a graphing calculator, all you need to do is to set up your table, type in the values close to the limit yuo want to evaluate, and plug in your function. If you are given a graph (like the one below), you just put a finger on a spot to the left and to the right of where you want to evaluate the limit. 

 If your fingers meet, then there is a limit and that is where it is.
      -So the limit as x approaches -4 of f(x) is equal  to 2 (point discontinuity).

If your fingers don't meet, then the limit DNE.
        -So the limit as x approaches 1 of f(x) of f(x) DNE because the left and right limits don't match (jump discontinuity).


Finally, to evaluate limits algebraically,we just use direct substitution, the dividing out/factoring method, or the rationalizing/conjugate method. For direct substitution, we just simply substitute the number is approaching into x and simplify to get the answer. However, if it ends up to be a number over 0, then it is undefined and the limit DNE because of unbounded behavior, If you end up with 0/0, then it is indeterminate and you must use either the factoring method or the rationalizing method next.

(http://www.onlinemathlearning.com/limits-calculus.html)

The dividing out/factoring method is just basically trying to factor the numerator and denominator to cancel some common terms to remove the zero, which is what is causing substitution to fail. Once you have the simplified expression, you just use direct substitution to solve.

(http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm)

And if direct substitution and the dividing out/factoring method both fail, then our final resort would be the rationalizing/conjugate method. We would just multiply the function by the conjugate of the denominator or the conjugate of numerator, depending on where the radical is. We would leave the non-conjugate part factored, since we want something to cancel.And we would just foil the multiplied conjugates, simplify, and eliminate any common factors in the numerator and denominator. Then, we just use direct substitution to solve for the answer.

(http://faculty.eicc.edu/bwood/math150supnotes/supplemental2.htm)

Works Cited:
http://www.mathsisfun.com/calculus/continuity.html
http://www.cwladis.com/math301/indeterminateforms.php
http://www.analyzemath.com/calculus/continuity/continuous_functions.html
http://www.onlinemathlearning.com/limits-calculus.html
http://tutorial.math.lamar.edu/Classes/CalcI/OneSidedLimits.aspx
http://nfva.info/LarsonCalc/Ch1_files/ch1_1_3w.htm
http://faculty.eicc.edu/bwood/math150supnotes/supplemental2.htm